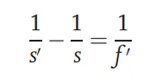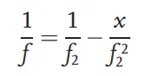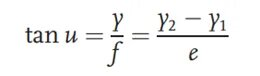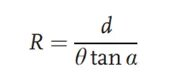Definice ohniskové vzdálenosti optických systémů a metody testování

1. Ohnisková vzdálenost optických systémů

Ohnisková vzdálenost je velmi důležitým ukazatelem optického systému. Pojmu ohniskové vzdálenosti víceméně rozumíme, proto si ho zde zopakujeme.
Ohnisková vzdálenost optického systému, definovaná jako vzdálenost od optického středu optického systému k ohnisku paprsku při dopadu rovnoběžného světla, je měřítkem koncentrace nebo divergence světla v optickém systému. Pro ilustraci tohoto konceptu používáme následující diagram.

Na výše uvedeném obrázku rovnoběžný paprsek dopadající z levého konce po průchodu optickou soustavou konverguje do obrazového ohniska F', zpětná prodlužovací čára sbíhajícího se paprsku se protíná s odpovídající prodlužovací čárou dopadajícího rovnoběžného paprsku v bodě a plocha, která tímto bodem prochází a je kolmá k optické ose, se nazývá zadní hlavní rovina, zadní hlavní rovina se protíná s optickou osou v bodě P2, který se nazývá hlavní bod (nebo optický střed), vzdálenost mezi hlavním bodem a obrazovým ohniskem, to je to, co obvykle nazýváme ohniskovou vzdáleností, celý název je efektivní ohnisková vzdálenost obrazu.
Z obrázku je také patrné, že vzdálenost od posledního povrchu optické soustavy k ohnisku F' obrazu se nazývá zadní ohnisková vzdálenost (BFL). Obdobně, pokud rovnoběžný paprsek dopadá z pravé strany, existují také pojmy efektivní ohniskové vzdálenosti a přední ohniskové vzdálenosti (FFL).

2. Metody testování ohniskové vzdálenosti

V praxi existuje mnoho metod, které lze použít k testování ohniskové vzdálenosti optických systémů. Na základě různých principů lze metody testování ohniskové vzdálenosti rozdělit do tří kategorií. První kategorie je založena na poloze obrazové roviny, druhá kategorie využívá vztah mezi zvětšením a ohniskovou vzdáleností k získání hodnoty ohniskové vzdálenosti a třetí kategorie využívá zakřivení vlnoplochy sbíhajícího se světelného paprsku k získání hodnoty ohniskové vzdálenosti.
V této části si představíme běžně používané metody pro testování ohniskové vzdálenosti optických systémů:

2.1CMetoda olimátoru

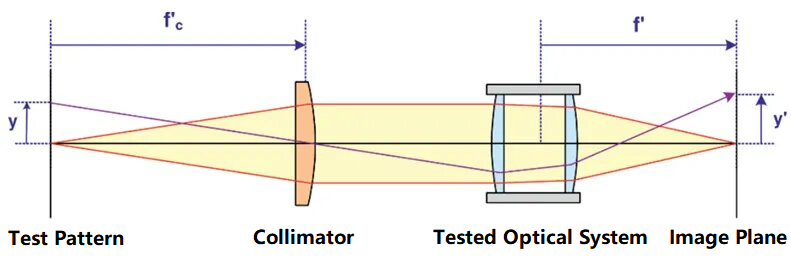
Princip použití kolimátoru k testování ohniskové vzdálenosti optického systému je znázorněn na níže uvedeném diagramu:

Na obrázku je testovací vzor umístěn v ohnisku kolimátoru. Výška y testovacího vzoru a ohnisková vzdálenost f_c' kolimátoru jsou známy. Poté, co je paralelní paprsek emitovaný kolimátorem konvergován testovaným optickým systémem a zobrazen v obrazové rovině, lze ohniskovou vzdálenost optického systému vypočítat na základě výšky y' testovacího vzoru v obrazové rovině. Ohniskovou vzdálenost testovaného optického systému lze vypočítat pomocí následujícího vzorce:

2.2 GaussovskáMmetoda
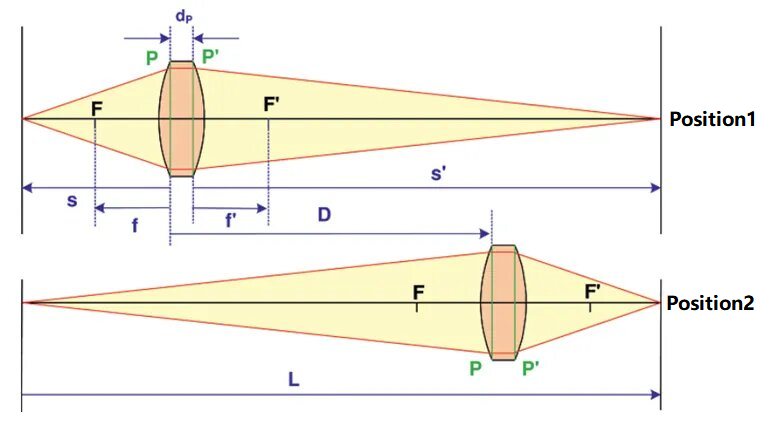
Schematický obrázek Gaussovy metody pro testování ohniskové vzdálenosti optického systému je znázorněn níže:

Na obrázku jsou přední a zadní hlavní rovina testovaného optického systému znázorněny jako P a P' a vzdálenost mezi těmito dvěma hlavními rovinami je d._PV této metodě je hodnota d_Pse považuje za známou, nebo je její hodnota malá a lze ji ignorovat. Objekt a přijímací stínítko jsou umístěny na levém a pravém konci a vzdálenost mezi nimi se zaznamená jako L, kde L musí být větší než 4násobek ohniskové vzdálenosti testovaného systému. Testovaný systém lze umístit do dvou poloh, označených jako poloha 1 a poloha 2. Objekt vlevo lze jasně zobrazit na přijímacím stínítku. Vzdálenost mezi těmito dvěma místy (označená jako D) lze změřit. Podle konjugovaného vztahu můžeme získat:

V těchto dvou polohách jsou vzdálenosti objektů zaznamenány jako s1 a s2, pak s2 - s1 = D. Odvozením vzorce můžeme získat ohniskovou vzdálenost optické soustavy takto:

2.3Lenzometr
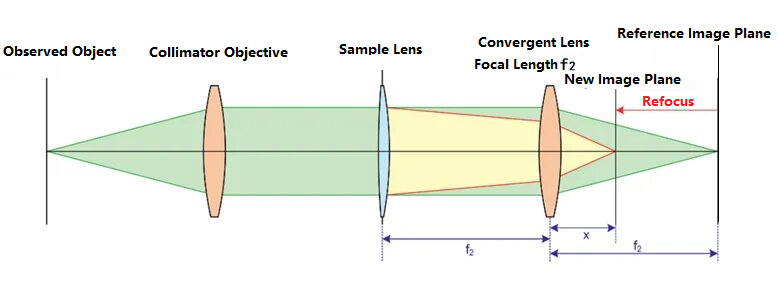
Lensometr je velmi vhodný pro testování optických systémů s dlouhou ohniskovou vzdáleností. Jeho schematický obrázek je následující:

Zaprvé, testovaná čočka není umístěna v optické dráze. Pozorovaný cíl vlevo prochází kolimační čočkou a stává se paralelním světlem. Rovnoběžné světlo je konvergováno spojkou s ohniskovou vzdáleností f.₂a vytváří jasný obraz v referenční obrazové rovině. Po kalibraci optické dráhy se testovaná čočka umístí do optické dráhy a vzdálenost mezi testovanou čočkou a spojkou je f₂V důsledku toho se vlivem testované čočky světelný paprsek znovu zaostří, což způsobí posun v poloze obrazové roviny a výsledkem bude jasný obraz v poloze nové obrazové roviny na diagramu. Vzdálenost mezi novou obrazovou rovinou a spojkou se označuje jako x. Na základě vztahu mezi objektem a obrazem lze ohniskovou vzdálenost testované čočky odvodit jako:

V praxi se čočkový měřič široce používá k měření horní ohniskové vzdálenosti brýlových čoček a má výhody jednoduchého ovládání a spolehlivé přesnosti.

2.4 AbbéRefraktometr

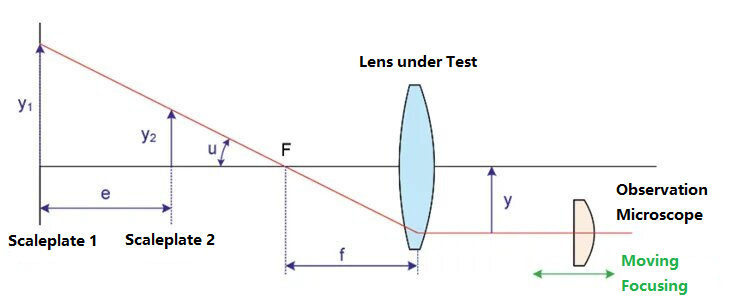
Abbeho refraktometr je další metodou pro testování ohniskové vzdálenosti optických systémů. Jeho schematický obrázek vypadá takto:

Na stranu s povrchem testované čočky, na které se nachází objekt, umístěte dvě pravítka s různou výškou, a to stupnici 1 a stupnici 2. Odpovídající výšky stupnic jsou y1 a y2. Vzdálenost mezi oběma stupnicemi je e a úhel mezi horní čarou pravítka a optickou osou je u. Stupnice je zobrazena testovanou čočkou s ohniskovou vzdáleností f. Na konci snímací plochy je instalován mikroskop. Změnou polohy mikroskopu se nacházejí horní obrazy obou stupnic. V tomto okamžiku se vzdálenost mezi mikroskopem a optickou osou označuje jako y. Podle vztahu mezi objektem a obrazem můžeme získat ohniskovou vzdálenost jako:

2.5 Moaré deflektometrieMetoda
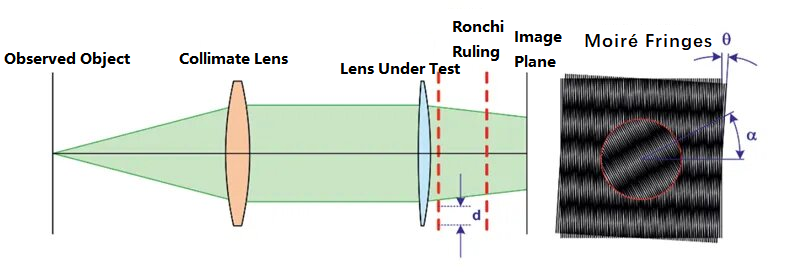
Metoda Moiré deflektometrie využívá dvě sady Ronchiho linek v paralelních světelných paprscích. Ronchiho linek je mřížkový vzor z chromového filmu naneseného na skleněný substrát, běžně používaný pro testování výkonu optických systémů. Metoda využívá změnu Moirého proužků tvořených dvěma mřížkami k testování ohniskové vzdálenosti optického systému. Schéma principu je následující:

Na obrázku výše se pozorovaný objekt po průchodu kolimátorem stává paralelním paprskem. V optické dráze, bez předchozího přidání testované čočky, prochází paralelní paprsek dvěma mřížkami s úhlem posunutí θ a roztečí mřížek d, čímž se na obrazové rovině vytvoří sada moaré proužků. Poté se do optické dráhy umístí testovaná čočka. Původní kolimované světlo po lomu čočkou vytvoří určitou ohniskovou vzdálenost. Poloměr zakřivení světelného paprsku lze získat z následujícího vzorce:

Testovaná čočka je obvykle umístěna velmi blízko první mřížky, takže hodnota R ve výše uvedeném vzorci odpovídá ohniskové vzdálenosti čočky. Výhodou této metody je, že umožňuje testovat ohniskovou vzdálenost systémů s kladnou i zápornou ohniskovou vzdáleností.

2.6 OptickýFiberAautokolimaceMmetoda
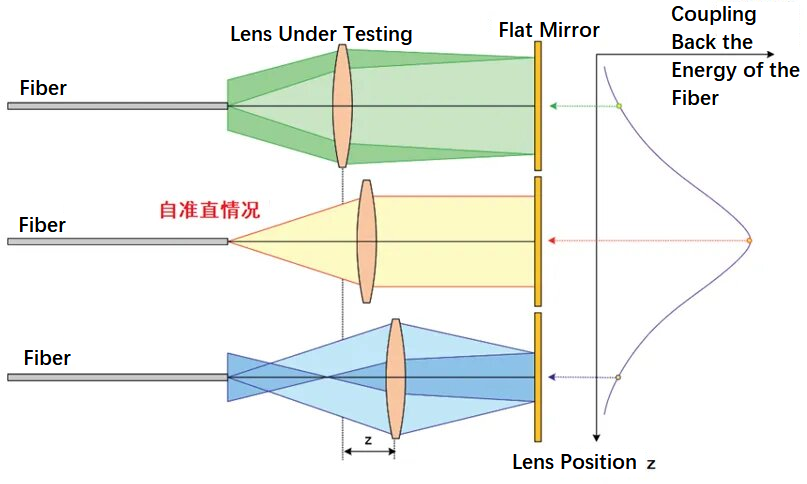
Princip použití metody autokolimace optických vláken k testování ohniskové vzdálenosti čočky je znázorněn na obrázku níže. Využívá optická vlákna k vyzařování divergentního paprsku, který prochází testovanou čočkou a poté dopadá na rovinné zrcadlo. Tři optické dráhy na obrázku představují stav optického vlákna v ohnisku, v ohnisku a vně ohniska. Pohybem testované čočky tam a zpět lze zjistit polohu hlavice vlákna v ohnisku. V tomto okamžiku je paprsek samokolimován a po odrazu od rovinného zrcadla se většina energie vrací do polohy hlavice vlákna. Metoda je v principu jednoduchá a snadno se implementuje.

3. Závěr

Ohnisková vzdálenost je důležitým parametrem optického systému. V tomto článku podrobně popíšeme koncept ohniskové vzdálenosti optického systému a metody jejího testování. V kombinaci se schematickým diagramem vysvětlíme definici ohniskové vzdálenosti, včetně konceptů ohniskové vzdálenosti na straně obrazu, ohniskové vzdálenosti na straně objektu a ohniskové vzdálenosti zepředu dozadu. V praxi existuje mnoho metod pro testování ohniskové vzdálenosti optického systému. Tento článek představuje principy testování kolimátorové metody, Gaussovy metody, metody měření ohniskové vzdálenosti, Abbéovy metody měření ohniskové vzdálenosti, metody Moiréova vychýlení a metody autokolimace optických vláken. Věřím, že přečtením tohoto článku lépe porozumíte parametrům ohniskové vzdálenosti v optických systémech.